Na temat obiektywów można dywagować godzinami. Który jest lepszy, który ma ciekawsze parametry, który jest bardziej przydatny w określonych warunkach… Producenci przekonują o niepowtarzalnych zaletach swoich produktów, kierując naszą uwagę na najlepsze techniczne cechy optyki, a ukrywając oczywiście te słabe. Prawa fizyki odnośnie optyki są znane i nic nie wskazuje na to, by na przestrzeni ostatnich dwóch wieków uległy zmianie. Jeśli chodzi o obiektywy, ich konstrukcję i koncepcję przy ich tworzeniu – zawsze dochodzimy do kompromisu pomiędzy jasnością, rozdzielczością a różnymi aberracjami.
Tekst: Jerzy Rudziński
Poniższy tekst jest skrótem tekstu, który ukazał się na łamach FilmPRO. Publikujemy go z drobnymi zmianami zostawiając esencję. Od chwili pojawienia się tekstu, tematyka, o której piszemy, nie straciła nic ze swojej aktualności.

Tablica testowa Ivana Putory
Nie udało się jeszcze wykonać uniwersalnego obiektywu do wszystkich zastosowań, a nasza ocena przydatności danego „szkła” z reguły jest subiektywna. Czasami kryteria wyboru optyki dla projektu filmowego osobom postronnym (i nie tylko) mogą wydawać się absurdalne z punktu widzenia technologii. Rezultat artystyczny tego, co zobaczymy na ekranie, jest w końcu najważniejszy.
Efektem ekranowym postrzegania ostrości jest wypadkowa suma rozdzielczości negatywu, obiektywu kamery, rozdzielczości pozytywu i rozdzielczości obiektywu projektora. Innymi słowy – każdy dodany element, środowisko – takie jak kolejne soczewki, nośniki i sama projekcja wpływają na właściwe (lub nie) postrzeganie ostrości.
(Przypomnijmy sobie tylko, jak wyglądają szybki rozdzielające salę projekcyjną od widowni. Notorycznie są zakurzone, brudne… a to też wpływa na ocenę tego, co widzimy na ekranie).
Suma rozdzielczości jest zawsze mniejsza od rozdzielczości pojedynczej składowej. Możemy to wyrazić bardzo uproszczonym wzorem, gdzie jednostką pomiarową są pary linii na milimetr lp/mm. Wzór wygląda tak:

I tak, gdy nasz negatyw ma 100 lp/mm, a obiektyw 50 lp/mm, to rozdzielczość naszego układu spadnie i wyniesie tylko 33 lp/mm (dla uproszczenia nie uwzględniamy rozdzielczości projektora).

Jeżeli użyjemy obiektywu o rozdzielczości np. 150 lp/mm, przy takim samym negatywie jak poprzednio, to otrzymamy:
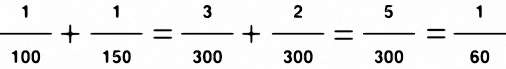
Rozdzielczość układu wyniesie 60 lp/mm.
Firmy produkujące materiały światłoczułe zalecały, aby rozdzielczość obiektywu była 3 razy większa od rozdzielczości negatywu. Jak nietrudno się domyślić, powyższy wzór na rozdzielczość sumaryczną układu negatyw + obiektyw jest również kluczem do wytłumaczenia zagadnienia rozdzielczości zachodzącego w kamerach cyfrowych i magii ilości pikseli.
A teraz trochę teorii. Proszę czytać cierpliwie. Zaraz się wszystko wyjaśni.
Rozdzielczość, jaką może odwzorować sensor, jest określona przez prawo Nyquista (tzw. częstotliwość Nyquista). Rozdzielczość, jaką teoretycznie może dać obiektyw – jest z kolei określona przez wzór matematyczny, zwany kryterium Rayleigh’a.

Częstotliwość Nyquista – to w uproszczeniu minimalna częstość pikseli na przetworniku (podana w ilości pikseli na mm), jaka jest potrzebna do zarejestrowania danej rozdzielczości (też nazywanej częstością). Rezultat dostajemy, gdy kierujemy kamerę na tablicę testową, na której widnieją równoległe naprzemienne czarne i białe linie. I analizujemy wynik. Przyjmuje się zatem, że aby sprostać rozdzielczości obiektywu wynoszącej np. 100 linii na mm (czyli 50 par linii na mm – 50 lp/mm), przetwornik musi mieć dwa razy więcej pikseli na milimetr liniowo, czyli 200 na mm (100 par pikseli/mm).
Kryterium Rayleigha określa teoretyczną maksymalną rozdzielczość, jaką daje obiektyw, biorąc pod uwagę prawa fizyki. Brzmi, jakby było skomplikowane, ale nie jest. Kryterium to jest wyrażone wzorem matematycznym i uwzględnia jedyny wchodzący w grę czynnik fizyczny, który powoduje, że obraz punktu dawany przez obiektyw nie jest punktem (jak to mówi geometria), tylko rozmytą plamką. Dodatkowo okoloną rozmytymi pierścieniami. Inaczej mówiąc – w efekcie końcowym obrazem punktu nie jest punkt, tylko plamka o pewnej średnicy.
Czynnikiem zamieniającym punkt na plamkę, czyli ograniczającym rozdzielczość, jest dyfrakcja, czyli ugięcie światła. To znamy ze szkoły i lekcji fizyki. A teraz coś nowego: plamka ta nazywa się dyskiem Airy’ego i jest środkową, zasadniczą częścią obrazu punktu – dawanego przez obiektyw – bez uwzględnienia pierścieni.
Niestety, na tym nie koniec. Musimy iść dalej, by przebrnąć przez te zawiłości i zrozumieć, o co chodzi: średnica tej centralnej plamki jest utożsamiana z rozdzielczością. Rozdzielczość ograniczona dyfrakcją zależy teoretycznie tylko od średnicy obiektywu, czyli w matematycznym uproszczeniu od liczby przysłony. Im mniejsza wartość przysłony (F 1.4), tym większa rozdzielczość. I odwrotnie – F 16 to mała rozdzielczość (ogniskowa obiektywu nie wpływa na rozdzielczość). Z kolei przysłona F 1.4 to duże aberracje optyczne, a F 16 to małe aberracje…
Jak się domyślacie, zależnie od użytej do testów optyki, kamery rezultaty wynikowe będą się od siebie znacznie różniły. Przy znanych warunkach brzegowych przeniesienia szczegółowości poprzez przetwornik, wynik niemal automatycznie staje się oczywisty. Matryca o rozdzielczości 200 pikseli mieszczących się w jednym milimetrze, daje 100 par pikseli na mm (czyli 100 lp/mm) i jest w stanie odwzorować rozdzielczość obiektywu 50 lp/mm. Jak widzimy, zbliżyliśmy się bardzo do wyniku sumarycznego rozważań negatyw + obiektyw, gdzie rozdzielczość obiektywu wynosiła 150 lp/mm. Z tych rozważań możemy wyciągnąć wniosek, że stosowanie obiektywu o dużej rozdzielczości w kamerach cyfrowych nie ma sensu…
Jednak jest to tylko część prawdy. Pamiętajmy, że wraz ze wzrostem przysłony do np. F 16 mamy znaczny spadek rozdzielczości.
O jeszcze jednej dość istotnej rzeczy warto pamiętać. Otóż przed matrycą jest zawsze umieszczony filtr rozostrzający, tzw. antyaliazingowy (lub też z angielska: Low Frequency Pass Filter). Jego zadaniem jest rozostrzenie punktu (linii), którego odwzorowanie na matrycy jest mniejsze od rozmiaru piksela.
W ten sposób mamy po drodze kolejny element, który wpływa na ostateczny wynik. Prześledźmy jeszcze sytuację, w której badamy trzy matryce, mające różne wymiary fizyczne. Umownie nazwijmy je: mała, średnia i duża matryca. W tym przykładzie wszystkie mają rozdzielczość 2K, czyli 2000 pikseli w podstawie klatki. Dla uproszczenia przyjmijmy, że mała matryca ma podstawę o długości 5 mm, średnia 10 mm, duża 20 mm. W małej matrycy przypada 400 pikseli na milimetr (2000 pikseli/5 mm), co daje nam 200 par pikseli/ mm. A zatem obiektyw zastosowany w tej kamerze powinien mieć minimalną rozdzielczość 100 lp/mm. W średniej matrycy przypada 200 pikseli/mm, co daje nam 100 par pikseli /mm – obiektyw powinien posiadać rozdzielczość 50 lp/mm. W dużej matrycy przypada 100 pikseli/mm (2000 pikseli /20 mm) – co daje nam 50 par pikseli/mm. Z tego wniosek, że obiektyw powinien posiadać minimalną rozdzielczość 25 lp/mm. Konkluzja jest zatem taka, że większa matryca może korzystać z „gorszych” obiektywów zupełnie spokojnie. Co kłóci się poniekąd ze zdrowym rozsądkiem, ale tak jest.
Warunki brzegowe dla dużych matryc ulegną poprawie, gdy podniesiemy ilość pikseli do 4K w linii podstawy. Wówczas minimalna rozdzielczość obiektywu powinna być 50 lp/mm. Stąd wniosek, słuszny zresztą – i producenci sprzętu o tym wiedzą, że wydłużanie podstawy kadru i PROPORCJONALNE zwiększanie ilości pikseli nie przyniesie nam zmiany rozdzielczości całego układu matryca + obiektyw. Natomiast podniesienie ilości pikseli i niepowiększanie rozmiaru klatki filmowej (czyli niejako gęstsze upakowanie pikseli w tym samym obszarze) zacznie stawiać większe wymagania w stosunku do optyki.
Naocznym przykładem jest tu zastosowanie matrycy o podstawie 5 mm o dużym zagęszczeniu pikseli w jednym milimetrze. Tutaj kryterium rozdzielczości dla użytego obiektywu wynosi minimum 100 lp/mm.
I jeszcze coś: Pamiętajmy, że wielkość halogenków srebra w taśmie filmowej jest stała w stosunku do użytego formatu, natomiast w matrycach cyfrowych rozmiar piksela jest zmienny w stosunku do formatu.
Producenci kamer podają nam hasło kamera HD, 2K, 4K… 8K – każda z tych kamer wymaga innego kryterium doboru rozdzielczości optyki w stosunku do wielkości klatki.

Bardzo często skupiamy się na jednym parametrze, zapominając o współzależności kilku parametrów, które tylko gdy są w całości wzięte pod uwagę, odpowiadają za ostateczny wynik i de facto jakość końcową. Pamiętam swoje zdziwienie, gdy do kamery z przetwornikiem 1/3” zastosowałem obiektyw przeznaczony do kamery z przetwornikiem 2/3”. Zamiast poprawy jakości obrazu uzyskałem efekt wręcz odwrotny… Próbując wytłumaczyć sobie zaistniałą sytuację, pomyślałem: zła kamera? Dopiero później przyszła refleksja.
Po pięćdziesięciu paru latach w erze kamer cyfrowych test Putory i idea stałego odniesienia w porównaniu układu sensor – obiektyw powróciła, dzięki zmęczonym operatorom zmuszonym do ciągłego przeliczania ilości pikseli w różnych matrycach w celu dowiedzenia się, co układ matryca + obiektyw pozwoli im uzyskać. Obecnie Test Ivana Putory zawiera parę dodatków, umożliwiających wsparcie w analizach komputerowych, z których możemy się dowiedzieć, gdzie znajdują się mielizny, czyli co dokładnie w danej konfiguracji odpowiada za jakość obrazu: kamera, obiektyw czy kodek. Ale i bez tych dodatków sama plansza testowa Putory jest nadal niezmiennie aktualna. I niezawodna.
Jeszcze słów kilka odnośnie przeprowadzania testów optyki. Bardzo często umieszczamy w kadrze jednocześnie parę tablic testowych: jedną w centrum kadru a pozostałe na bokach. Z reguły są przyklejone do ściany. W ten sposób chcemy się dowiedzieć, jaka rozdzielczość jest w centrum, a jaka na skrajach kadru. Wynik tak przeprowadzonego testu może ulec zmianie, gdy zachowamy stałą odległość tablic w stosunku do obiektywu, tzn. gdy ustawimy je NIE NA ŚCIANIE, a na linii OKRĘGU a obiektyw będzie w centrum koła. Logiczne, ale często się o tym zapomina, i potem ocena danego zestawu obiektywów jest niewłaściwa.
Z drugiej strony, coraz częściej wybór optyki podlega różnym zewnętrznym czynnikom i staje się w związku z tym bardzo subiektywny. Brak wiedzy na temat całego kontekstu podjęcia decyzji o wyborze konkretnego szkła, może zniechęcać innych. Subiektywna opinia, czyli ta, która jest najmocniejsza emocjonalnie, rzucona np. podczas niezobowiązującej rozmowy, idzie w świat… i w skrajnym wypadku całkowicie wypacza rzeczową informację o produkcie.
Przykład: ostatnio dwóch operatorów niezależnie od siebie przeprowadzało test tego samego obiektywu, na tej samej kamerze z matrycą super 35. Obaj orzekli, że obiektyw jest zły. Na pytanie: „Dlaczego”? Pierwszy z nich powiedział: „Bo jest za ciężki”. Drugi: „Bo jest zbyt perfekcyjny…”.
Ciekaw jestem, co by na to powiedzieli lord Rayleigh, Harry Nyquist i Ivan Putora…


